Rahimi, Reza1; Fenton, Gordon A.2 and Liu, Yi3
1 Research Assistant, Department of Civil and Resource Engineering, Dalhousie University, 5248 Morris St., Halifax, NS, Canada, reza.rahimi@dal.ca
2 Professor, Department of Engineering Mathematics, Dalhousie University, 5269 Morris St., Halifax, NS, Canada, gordon.fenton@dal.ca
3 Professor and Department Head, Department of Civil and Resource Engineering, Dalhousie University, 5248 Morris St., Halifax, NS, Canada, yi.liu@dal.ca
ABSTRACT
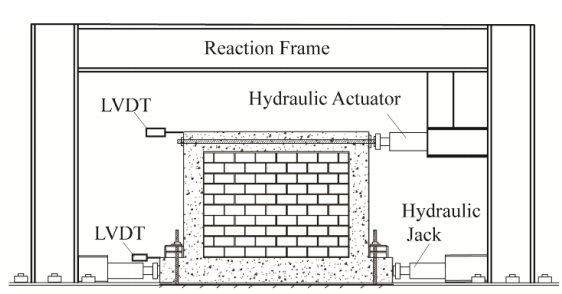
This paper presents a study on the probability distribution of the lateral strength of unreinforced masonry (URM) infill walls bounded by reinforced concrete (RC) frames. Based on the load and
resistance factor design (LRFD) procedure for URM, the failure probability of the system was studied. The distribution of the lateral strength is a key component of such a probability estimate. To determine this distribution, the compressive strength, ݂ ᇱ , of the URM infill wall was modeled as a continuous spatially variable random field. Based on ݂ ᇱ , other mechanical properties of masonry, such as the elastic modulus as well as the ultimate strain and the corresponding stress, were determined using established relationships including a random model error component. A finite element model employing shell elements using the OpenSEES program was used to calculate the lateral strength of the infill and the lateral load vs. displacement behaviour of the infill system. The Monte-Carlo simulation method was then used to produce histograms of lateral strength, over a range of statistics (mean, standard deviation, and correlation length) of ݂ ᇱ . A fitted strength distribution was then determined and its application in calculation of failure probabilities of the masonry infilled frames was proposed.
042