Pari, Manimaran1; Hendriks, M.A.N2 and Rots, J.G3
1 PhD Researcher, Delft University of Technology, The Netherlands, M.Pari@tudelft.nl
2 Assoc. Professor, Delft University of Technology, The Netherlands & Professor, Norwegian University of Science and Technology, Norway, M.A.N.hendriks@tudelft.nl
3 Professor, Delft University of Technology, The Netherlands, J.G.Rots@tudelft.nl
ABSTRACT
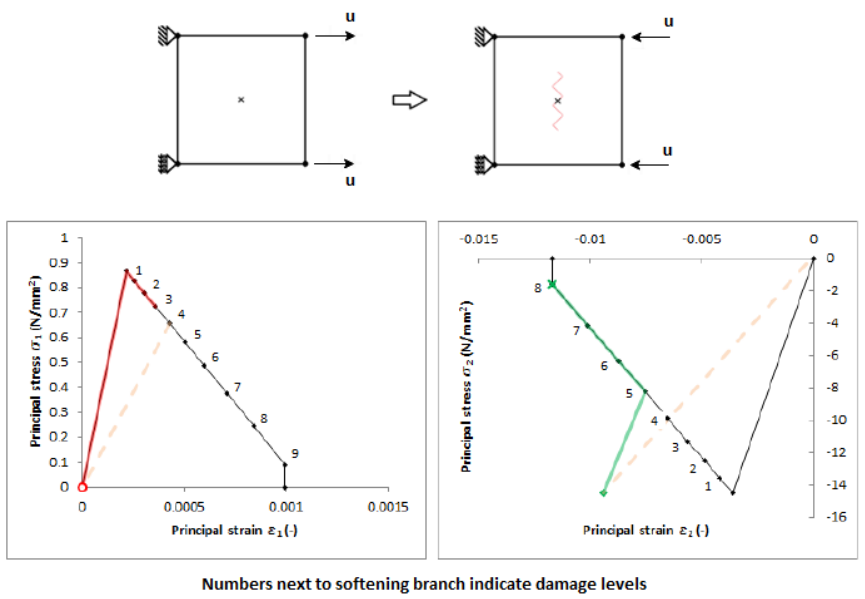
Finite element models, in use for simulation of materials characterised by brittle failure like masonry, often encounter problems related to snap back, bifurcation points, divergence or material softening leading to negative tangent stiffness and the consequent ill conditioning of the formulation. Serious convergence issues led to quite inaccurate results due to large deviation from tolerance norms. This gave rise to several non-iterative total approaches one of which is the Sequentially Linear Analysis (SLA), which has been in development from the early 2000s. The SLA is an event-by-event strategy, where a sequence of scaled linear analyses is performed, coupled with decreasing secant stiffness and strength at the critical integration point in the model. The use of positive secant branches, damage increments, and multiple integration points not entering into failure, makes this method robust and devoid of convergence troubles. Originally implemented within the scope of the smeared crack approach in a plane stress context, the method has undergone several developments over the years and an overview is presented in this article. But there are impending issues/areas to be addressed within the framework to make it a serious practical alternative to popular non-linear incremental-iterative methods like the Newton Raphson method. In SLA, an integration point softening in tension or compression, when subject to a reversal of stress states as in the case of a closing crack reloaded in compression, does not regain the original stiffness upon stress reversal. Stress reversal is quite common in cyclic loading but is also observed in monotonic cases when stress redistribution occurs. Currently, applications of SLA are limited to monotonic loading and this article illustrates the stress reversal problem with a monotonic analysis on a Calcium silicate masonry wall tested at TU Delft under the research program in relation to induced seismicity in Groningen, The Netherlands. A solution strategy to overcome the issue is proposed and outlined, with validation studies to follow in the near future.
060